IonnKorr: Electromagnetism a la Mendeleev

Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο23-

Αναζήτηση
"κρυμμένων" Διαστάσεων
(ε' μέρος)

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Στο προηγούμενο μέρος είχαμε καταλήξει στο συμπέρασμα
ότι ο συμπληρωματικός Φασματικός Χωρόχρονος
πρέπει μάλλον να έχει ως διαστάσεις
(με βάση την εργασία του Hamilton το 1827)
τις τρεις ορμές (Px, Py, Pz) και την Ενέργεια (E) ενός φυσικού συστήματος.

${\vec {P}}={\begin{bmatrix}P_{x}\\P_{y}\\P_{z}\\E/c\end{bmatrix}}$

Προσθήκη λεζάντας

Όμως ...
ένας Χώρος με συντεταγμένες φυσικά μεγέθη όπως η Ορμή (P) μπορεί, βέβαια, να είναι σωστός ως τεχνικό "μαθηματικό κατασκεύασμα"
αλλά δεν μπορεί να θεωρηθεί ως "Γεωμετρικός Χώρος"

Αυτό που θα θέλαμε είναι μία "γεωμετρικοποίηση" (ή αλλιώς "αφυλοποίηση")
των τεσσάρων αυτών συνιστωσών Px, Py, Pz, E
ώστε να απογυμνωθούν από το "φυσικό περιεχόμενό" τους
και να εκφραστούν σε meters
ώστε να μπορούν να χρησιμοποιηθούν ως διαστάσεις
ενός διευρυμένου συμπληρωματικού χώρου.

Έτσι η κατάσταση πάγωσε για έναν περίπου αιώνα.

Η κατάσταση άλλαξε με την εμφάνιση της Κβαντικής Θεωρίας

Το πρώτο μεγάλο βήμα έγινε από τον Max Planck
στην αρχή του 19ου αιώνα (περί το 1900).

Max Planck
(1858 - 1947)
Ένας από τους πατέρες της Κβαντικής Φυσικής
----
Που να το φανταζόταν
ότι η εργασία του
θα άνοιγε τον δρόμο
για τον 11-δάστατο Χωρόχρονο της Χορδοθεωρίας

Αυτός θεώρησε ένα σωματίδιο (δηλ. το φωτόνιο) ως "υλοκύμα"
και έτσι μπόρεσε να ανακαλύψει μία σχέση
που κάνει ακριβώς ότι ζητάμε.

Με την περίφημη Σχέση Planck,
η Ενέργεια (Ε) ενός φωτονίου
συνδέεται με
την Συχνότητα (ω) του "υλοκύματος" που το αντιπροσωπεύει.

$E=\hbar \cdot \omega$

Προσθήκη λεζάντας

Το δεύτερο μεγάλο βήμα έγινε από τον Louis De Broglie

Louis de Broglie
(1892 - 1987)
Ένας από τους πατέρες της Κβαντικής Φυσικής
-----
Που να το φανταζόταν
ότι η εργασία του
θα άνοιγε τον δρόμο
για τον 11-διάστατο Χωρόχρονο της Χορδοθεωρίας

Και αυτός, αντίστοιχα, θεώρησε
ένα σωματίδιο (δηλ. το φωτόνιο) ως "υλοκύμα"
και έτσι μπόρεσε να ανακαλύψει μία σχέση
που κάνει ακριβώς ότι ζητάμε.

Με την περίφημη Σχέση deBroglie,
η Ορμή (P) ενός φωτονίου
συνδέεται με
την κυματοδιάνυσμα (k) του "υλοκύματος" που το αντιπροσωπεύει.

${\vec {P}}=\hbar \cdot {\vec {k}}$

όπου:
P = Ορμή
k = κυματοδιάνυσμα
h = σταθερά Planck

Αναλυτικότερα, η παραπάνω σχέση γράφεται:

${\vec {k}}={\begin{bmatrix}k_{x}\\k_{y}\\k_{z}\\\end{bmatrix}}$

Προσθήκη λεζάντας

Οπότε έχουμε τις εξισώσεις

${\overrightarrow {P}}={\begin{cases}{\color {cyan}{E/c}}=\hbar \cdot {\color {cyan}{\omega /c}}\\{\color {blue}{P_{x}}}=\hbar \cdot {\color {blue}{k_{x}}}\\{\color {blue}{P_{y}}}=\hbar \cdot {\color {blue}{k_{y}}}\\{\color {blue}{P_{z}}}=\hbar \cdot {\color {blue}{k_{z}}}\\\end{cases}}$

όπου:
Px, Py, Pz = οι τρεις συνιστώσες της Ορμής (P)
kx, ky, kz = οι τρείς συνιστώσες του Κυματοδιανύσματος (k)
και h = η σταθερά του Planck

Η σταθερά Planck που έχει μία απίστευτα μικρή τιμή

παίζει έναν κομβικό ρόλο στην Φυσική.
Εδώ, επικεντρωνόμαστε στην μοναδική ιδιότητά της
να "απορροφά" το φυσικό περιεχόμενο των Φυσικών Μεγεθών
(π.χ. Ενέργεια, Ορμή, Στροφορμή κλπ)
και τα "απογυμνώνει", μετατρέποντάς τα σε Γεωμετρικά Μεγέθη.

$h = 6,6 \cdot 10^{-34}\ \frac {\mbox{kg} \cdot m^{2}} {s}$

Μονάδες
της Σταθεράς Planck
------------------------------------
Kg = χιλιόγραμμο
m = μέτρο
s = δευτερόλεπτο

Με άλλα λόγια, η σταθερά Planck
"αποφλοιώνει" τα Φυσικά Μεγέθη από το υλικό τους περιτύλιγμα
αλλά αφήνει ανεπηρέαστη και άθικτη την γεωμετρική τους υφή.
Έτσι δίνεται η δυνατότητα
να λάβουμε ως διαστάσεις του συμπληρωματικού Φασματικού Χώρου
τις συνιστώσες του κυματοδιανύματος (kx, ky, kz)

Αν τώρα προσθέσουμε
και την κυκλική συχνότητα (ω) ως τέταρτη συνιστώσα
στις συνιστώσες του κυματοδιανύματος (k)
τότε οι διαστάσεις του Φασματικού Χωρόχρονου
που γράψαμε στην αρχή της σελίδας
αντικαθίστανται από

${\vec {k}}={\begin{bmatrix}\color {blue}{k_{x}}\\\color {blue}{k_{y}}\\\color {blue}{k_{z}}\\\color {Cyan}{\omega /c}\end{bmatrix}}$

Προσθήκη λεζάντας

Είναι απόλυτα αδύνατο να σχηματοποιήσουμε
τον νέο αυτόν Χωρόχρονο
μέσα στον συνήθη, "δικό μας", Πραγματικό Χωρόχρονο

Πάντως ένα σχήμα που δίνει μια κάποια "ιδέα" είναι το εξής

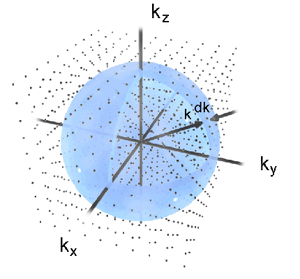Μία αναπαράσταση
των αξόνων του Φασματικού Χώρου
που ονομάζεται και
k-Χώρος
ή
Αντίστροφος (reciprocal) Χώρος

Το βέβαιο είναι ότι
ο νέος αυτός Χωρόχρονος έχει "δυικές ιδιότητες" σε σχέση
με τον συνήθη, "δικό μας", Πραγματικό Χωρόχρονο
Ένα σχήμα που υποτίθεται ότι δίνει μία ιδέα
της συμμετρίας των δύο αυτών Χωρόχρονων είναι το εξής

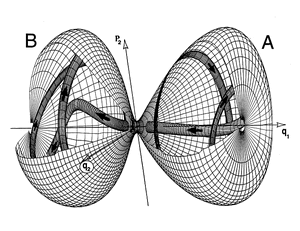Στο σχήμα αυτό
παρουσιάζεται ένας υπόχωρος των δύο Χωροχρόνων
που απαρτίζεται
από δύο διαστάσεις (q1, q2) του Πραγματικού Χωρόχρονου
και μία διάσταση (p3) του Φασματικού

Όμως και πάλι δεν φτάσαμε στον πλήρη προσδιορισμό
των νέων διαστάσεων που ζητάμε
Αυτό θα γίνει στο επόμενο μέρος.

-------------------------------------------------------------------
Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------