Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο21-
Αναζήτηση
"κρυμμένων" Διαστάσεων
(γ' μέρος)
"κρυμμένων" Διαστάσεων
(γ' μέρος)
--------------------------------------------------------------------
--------------------------------------------------------------------
Στο προηγούμενο μέρος, αναφερθήκαμε στο
"Πρόβλημα του Ναυαγοσώστη του Feynman" και την
"επιλογή της ελάχιστης διαδρομής από τα μυρμήγκια"
ως ενδείξεις για την πιθανότητα να υπάρχουν "κρυμμένες διαστάσεις"
που να σχετίζονται με την ταχύτητα.
Περιληπτικά, αναφέρουμε ότι τόσο ο άνθρωπος
όσο και το μυρμήγκι
μπορούν να προσδιορίσουν την γραμμή "Ελαχίστου Χρόνου"
όταν ο Χώρος κατέχεται από δύο διαφορετικά υλικά μέσα:
- ο μεν άνθρωπος μέσω της Φυσικής (όπως εξηγείται αμέσως παρακάτω)
- το δε μυρμήγκι επειδή ενδεχομένως έχει το σχετικό όργανο
(ανάλογο με το sonar των νυχτερίδων
και την πλάγια γραμμή των ψαριών)
Πράγματι, με βάση τον νόμο του Snell
(που προκύπτει από την περίφημη Αρχή του Fermat)
αν γνωρίζουμε τους δύο συντελεστές (η) και την μία γωνία (θ1)
μπορούμε να βρούμε την άλλη γωνία (θ2)
και έτσι να σχεδιάσουμε την ιδανική διαδρομή.
Μέχρις εδώ, θα μπορούσε να πει κάποιος,
ότι δεν τίθεται ζήτημα επέκτασης των Διαστάσεων
Όμως...
υπάρχει και το αντίστοιχο φαινόμενο (διάθλαση) με το φως (π.χ. με ένα φωτόνιο)
Ε ... και τώρα μπαίνει το τεράστιο ερώτημα.
Με ποιές δυνατότητες μπορεί ένα φωτόνιο να επιλέξει διαδρομές?
Αν θέλουμε να διατηρήσουμε τον Ευκλείδειο Χώρο μας
(δηλ. τον Χωρόχρονο AdS, στην γενικότερη περίπτωση)
ως τον ορθό αντιπρόσωπο του Φυσικού Χώρου που ζούμε
πρέπει να δεχθούμε
ότι, ναι, το φωτόνιο
και κρίνει διαδρομές και υπολογίζει γωνίες.
Αν, όμως, θέλουμε να αποφύγουμε τους παραλογισμούς
τότε η λύση είναι μία:
Ότι το φωτόνιο δεν κάνει καμία επιλογή
καθόσον δεν αντιμετωπίζει κανένα δίλημμα!
Απλά, συνεχίζει να κινείται σε "ευθεία γραμμή"
η οποία είναι ταυτόχρονα και
γραμμή Ελάχιστου Μήκους και Ελάχιστου Χρόνου και Ελάχιστης Αντίστασης.
Πως είναι δυνατόν κάτι τέτοιο?
Απλά, το φωτόνιο δεν κινείται στον Ευκλείδειο Χώρο
(που ο άνθρωπος αντιλαμβάνεται ως Φυσικό Χώρο)
αλλά σε έναν γενικότερο χώρο που περιλαμβάνει και τις ταχύτητες.
Απαιτείται, επομένως, η επέκταση του Χώρου
με Διαστάσεις που σχετίζονται με την ταχύτητα
ή αλλιώς, η αποδοχή ότι ο Φασικός Χώρος
είναι ο ορθός αντιπρόσωπος του Φυσικού Χώρου που ζούμε
Υπενθυμίζουμε ότι:
ΕΠΛΟΓΟΣ:
Εντυπωσιακό είναι το γεγονός
ότι οι Άνθρωποι αγκιστρώνονται στο είδος του Μαθηματικού Χώρου
που κληρονόμησαν από τους προηγούμενους,
θεωρώντας ότι αυτό αντιπροσωπεύει τον Φυσικό Χώρο της Πραγματικότητας,
με μεγαλύτερη ευλάβεια και αφοσίωση
ακόμη και από την Πατρίδα τους και την Θρησκεία τους.
Ενδεικτικό είναι το γεγονός ότι
για 100.000 χρόνια και πλέον
ο Άνθρωπος συνέχιζε να πιστεύει ότι η Γη είναι επίπεδη
παρά το γεγονός ότι
και χωρίς την χρήση του όποιου μαθηματικού ή επιστημονικού εργαλείου
φαινόταν, περίτρανα, ότι ήταν στρογγυλή.
Αυτή η "διεύρυνση του Ορίζοντα" για υψηλότερους Παρατηρητές
θα είχε γίνει αντιληπτή από δεκάδες χιλιάδες ανθρώπους επί 100.000 χρόνια
Ωστόσο, η εμμονή στην Επιπεδότητα ήταν κάτι παραπάνω από ιερή.
(Θα προτιμούσαν να αποδώσουν το φαινόμενο αυτό
σε κάποια παραδοξότητα του Ορίζοντα π.χ. "παράδοξο του Ορίζοντα"
παρά να αποδεχθούν την Σφαιρικότητα)
Μόνον, εντελώς, απτές αποδείξεις των δύο πρόσφατων χιλιετιών
μπόρεσαν να την γκρεμίσουν.
Στο προηγούμενο μέρος, αναφερθήκαμε στο
"Πρόβλημα του Ναυαγοσώστη του Feynman" και την
"επιλογή της ελάχιστης διαδρομής από τα μυρμήγκια"
ως ενδείξεις για την πιθανότητα να υπάρχουν "κρυμμένες διαστάσεις"
που να σχετίζονται με την ταχύτητα.
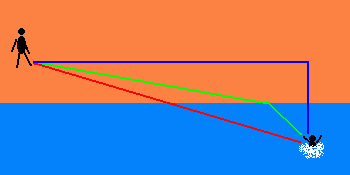 |
| Υπάρχουν άπειρες διαδρομές που ενώνουν τον Ναυαγοσώστη (ή αντίστοιχα, την Μυρμηγκοφωλιά) με τον Ναυαγό (ή αντίστοιχα, με την Μυρμηγκοτροφή) Ωστόσο, τρεις είναι ξεχωριστές: - Η κυανή γραμμή είναι της Ελάχιστης Αντίστασης (εφόσον το μεγαλύτερο μέρος της βρίσκεται στην παραλία με τον μικρότερο συντελεστή τριβής) - Η πράσινη γραμμή είναι του Ελάχιστου Χρόνου (η οποία και είναι η προτιμώμενη) - Η ερυθρή γραμμή είναι του Ελάχιστου Μήκους |
Περιληπτικά, αναφέρουμε ότι τόσο ο άνθρωπος
όσο και το μυρμήγκι
μπορούν να προσδιορίσουν την γραμμή "Ελαχίστου Χρόνου"
όταν ο Χώρος κατέχεται από δύο διαφορετικά υλικά μέσα:
- ο μεν άνθρωπος μέσω της Φυσικής (όπως εξηγείται αμέσως παρακάτω)
- το δε μυρμήγκι επειδή ενδεχομένως έχει το σχετικό όργανο
(ανάλογο με το sonar των νυχτερίδων
και την πλάγια γραμμή των ψαριών)
| Η ιδανική διαδρομή (αυτή που διαρκεί Ελάχιστο Χρόνο) σε ένα Χώρο που κατέχεται από δύο Υλικά Μέσα καθορίζεται από δύο γωνίες και τους δύο συντελεστές τριβής (η1) και (η2) των δύο υλικών |
Πράγματι, με βάση τον νόμο του Snell
(που προκύπτει από την περίφημη Αρχή του Fermat)
αν γνωρίζουμε τους δύο συντελεστές (η) και την μία γωνία (θ1)
μπορούμε να βρούμε την άλλη γωνία (θ2)
και έτσι να σχεδιάσουμε την ιδανική διαδρομή.
| Το 1 είναι το "αραιό" μέσο (με την μικρή αντίσταση στην κίνηση) ενώ το 2 είναι το "πυκνό" μέσο (με την μεγάλη αντίσταση στην κίνηση) |
 |
| Pierre de Fermat (1661 - 1665) Γάλλος μαθηματικός Ασχολήθηκε με προβλήματα ελαχίστων και την Οπτική ------ Ποτέ δεν θα μπορούσε να φανταστεί ότι η θεωρία του θα μπορούσε να ανοίξει τον δρόμο για την αύξηση των Διαστάσεων του Χώρου και του Χρόνου |
Μέχρις εδώ, θα μπορούσε να πει κάποιος,
ότι δεν τίθεται ζήτημα επέκτασης των Διαστάσεων
Όμως...
υπάρχει και το αντίστοιχο φαινόμενο (διάθλαση) με το φως (π.χ. με ένα φωτόνιο)
 |
| Ένα φωτόνιο εκκινεί από την Πηγή (π.χ. η λάμπα κάτω δεξιά) και καταλήγει σε έναν Ανιχνευτή (π.χ. έναν οφθαλμό άνω αριστερά) Αυτό που γνωρίζουμε όλοι είναι ότι το φωτόνιο (από τις άπειρες διαδρομές που συνδέουν την πηγή με τον ανιχνευτή) "επιλέγει" αυτήν του Ελαχίστου Χρόνου (δηλ. την πράσινη γραμμή) |
Ε ... και τώρα μπαίνει το τεράστιο ερώτημα.
Με ποιές δυνατότητες μπορεί ένα φωτόνιο να επιλέξει διαδρομές?
Έχει το φωτόνιο εγκέφαλο για να κρίνει διλήμματα
και πολύ περισσότερο
να λύνει εξισώσεις ώστε να επιλέξει
την ιδανική διαδρομή??
Αν θέλουμε να διατηρήσουμε τον Ευκλείδειο Χώρο μας
(δηλ. τον Χωρόχρονο AdS, στην γενικότερη περίπτωση)
ως τον ορθό αντιπρόσωπο του Φυσικού Χώρου που ζούμε
πρέπει να δεχθούμε
ότι, ναι, το φωτόνιο
και κρίνει διαδρομές και υπολογίζει γωνίες.
Αν, όμως, θέλουμε να αποφύγουμε τους παραλογισμούς
τότε η λύση είναι μία:
Ότι το φωτόνιο δεν κάνει καμία επιλογή
καθόσον δεν αντιμετωπίζει κανένα δίλημμα!
Απλά, συνεχίζει να κινείται σε "ευθεία γραμμή"
η οποία είναι ταυτόχρονα και
γραμμή Ελάχιστου Μήκους και Ελάχιστου Χρόνου και Ελάχιστης Αντίστασης.
Πως είναι δυνατόν κάτι τέτοιο?
Απλά, το φωτόνιο δεν κινείται στον Ευκλείδειο Χώρο
(που ο άνθρωπος αντιλαμβάνεται ως Φυσικό Χώρο)
αλλά σε έναν γενικότερο χώρο που περιλαμβάνει και τις ταχύτητες.
Απαιτείται, επομένως, η επέκταση του Χώρου
με Διαστάσεις που σχετίζονται με την ταχύτητα
ή αλλιώς, η αποδοχή ότι ο Φασικός Χώρος
είναι ο ορθός αντιπρόσωπος του Φυσικού Χώρου που ζούμε
Υπενθυμίζουμε ότι:
Φασικός Χώρος
=
=
πραγματικός χώρος
(δηλ. ο Χωρόχρονος AdS)
(δηλ. ο Χωρόχρονος AdS)
+
φανταστικός χώρος
(δηλ. ο Φασματικός χώρος με διαστάσεις τις ταχύτητες)
φανταστικός χώρος
(δηλ. ο Φασματικός χώρος με διαστάσεις τις ταχύτητες)
ΕΠΛΟΓΟΣ:
Εντυπωσιακό είναι το γεγονός
ότι οι Άνθρωποι αγκιστρώνονται στο είδος του Μαθηματικού Χώρου
που κληρονόμησαν από τους προηγούμενους,
θεωρώντας ότι αυτό αντιπροσωπεύει τον Φυσικό Χώρο της Πραγματικότητας,
με μεγαλύτερη ευλάβεια και αφοσίωση
ακόμη και από την Πατρίδα τους και την Θρησκεία τους.
Ενδεικτικό είναι το γεγονός ότι
για 100.000 χρόνια και πλέον
ο Άνθρωπος συνέχιζε να πιστεύει ότι η Γη είναι επίπεδη
παρά το γεγονός ότι
και χωρίς την χρήση του όποιου μαθηματικού ή επιστημονικού εργαλείου
φαινόταν, περίτρανα, ότι ήταν στρογγυλή.
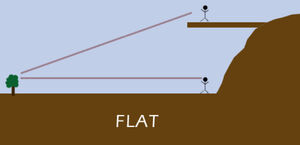 |
| Αν η Γη ήταν επίπεδη τότε κάθε αντικείμενο στο Ορίζοντα π.χ. ένα δέντρο θα έπρεπε να είναι ορατό από οποιοδήποτε ύψος και να βρισκόταν ο Παρατηρητής (ειδικά, ο χαμηλότερος Παρατηρητής θα είχε ευκρινέστερη θέαση) |
 |
| Ωστόσο επειδή η Γη είναι στρογγυλή ένα αντικείμενο στον Ορίζοντα ενώ είναι ορατό από τον υψηλότερο Παρατηρητή είναι αόρατο στον χαμηλότερο. |
θα είχε γίνει αντιληπτή από δεκάδες χιλιάδες ανθρώπους επί 100.000 χρόνια
Ωστόσο, η εμμονή στην Επιπεδότητα ήταν κάτι παραπάνω από ιερή.
(Θα προτιμούσαν να αποδώσουν το φαινόμενο αυτό
σε κάποια παραδοξότητα του Ορίζοντα π.χ. "παράδοξο του Ορίζοντα"
παρά να αποδεχθούν την Σφαιρικότητα)
Μόνον, εντελώς, απτές αποδείξεις των δύο πρόσφατων χιλιετιών
μπόρεσαν να την γκρεμίσουν.
-------------------------------------------------------------------
--------------------------------------------------------------------

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου