Ηλεκτρομαγνητισμός αλά Mendeleev
-C-02-
--------------------------------------------------------------------
--------------------------------------------------------------------
Όπως αναφέραμε στο προηγούμενο Μέρος C-01,
η "αρχειοθέτηση" σε πίνακες (Μέρος B-12a και Μέρος B-12b)
των Φυσικών Μεγεθών και των Φυσικών Νόμων
του Ηλεκτρομαγνητισμού, με βάση την Γεωμετροποίηση,
διαθέτει μία εξαιρετική αρμονία
(καθώς εμπεριέχει πολλές μαθηματικές συμμετρίες)
Όμως, η εμπλοκή του Χρόνου
αλλάζει ριζικά αυτήν την εικόνα
και κλονίζει "συθέμελα" την Γεωμετροποίηση.
Ας δούμε γιατί συμβαίνει αυτό.
Η "καταστροφή" οφείλεται
στην ανακάλυψη δύο κρίσιμων φαινομένων
- του φαινομένου της Ηλεκτρικής Μετατόπισης
(ή ορθότερα Φορτιακής Επαγωγής)
(ανακαλύφθηκε το 1861, από τον Maxwell)
- και του φαινομένου της Μαγνητικής Επαγωγής
(ανακαλύφθηκε το 1831 από τον Faraday)
1) Σύμφωνα με το Φαινόμενο της Ηλεκτρικής Μετατόπισης
που συμβαίνει σε έναν Πυκνωτή:
"Χρονικά μεταβαλλόμενο Ηλεκτρικό Φορτίο, δημιουργεί Ηλεκτρικό Ρεύμα"
2) Σύμφωνα με το Φαινόμενο της Μαγνητικής Επαγωγής
που συμβαίνει σε ένα Πηνίο:
"Χρονικά μεταβαλλόμενο Μαγνητικό Πεδίο, δημιουργεί Ηλεκτρικό Πεδίο"
- Ωραία, θα πει κάποιος, και ποιές είναι επιπτώσεις
αυτών των δύο φαινομένων?
Η πρώτη επίπτωση είναι ευπρόσδεκτη
και αναμενόμενη κατά κάποιον τρόπο
Αφορά την φύση ( = υφή) των "κβάντων" των 4 Οντοτήτων
Δηλαδή:
Δεν υπάρχει, πλέον,
- διάκριση μεταξύ "ακινήτων" και "κινούμενουν" ηλεκτρονίων
καθώς επίσης,
- ούτε και διάκριση μεταξύ "ακινήτων" και "κινούμενουν" φωτονίων
Ας δούμε τώρα ποιά είναι η επίπτωση στους Φυσικούς Νόμους
Όπως είναι λογικό, δεν υπάρχει καμία επίπτωση στους 8 Νόμους Σύνδεσης
και έτσι ο Πίνακας 1 μένει όπως έχει
Δεν υπάρχει επίπτωση στους Νόμους (Πεδιακούς και Διατήρησης)
του Ηλεκτρικού Φορτίου και του Μαγνητικού Πεδίου
κάτι που επίσης είναι αυτονόητο
καθώς δεν μπορούν να φυτρώνουν (ή να χάνονται)
- ούτε ηλεκτρόνια, δηλ. Ύλη
- ούτε φωτόνια, δηλ. Ενέργεια
από το (ή στο) "Πουθενά".
Οπότε, λογικά, οι δύο Φυσικοί Νόμοι (eq. 09 και eq. 11) του Πίνακα 2
(καθώς και οι 2x3 = 6 αντίστοιχοί τους από τους Πίνακες 3 και 4)
να παραμένουν ως έχουν
Υπάρχουν όμως επιπτώσεις στους Νόμους (Πεδιακούς και Διατήρησης)
του Ηλεκτρικού Ρεύματος και του Ηλεκτρικού Πεδίου.
Αυτοί που επηρεάζονται από τα δύο Φαινόμενα
είναι οι άλλοι δύο Φυσικοί Νόμοι του Πίνακα 2
(καθώς και οι 2x3 = 6 αντίστοιχοί τους από τους Πίνακες 3 και 4)
Σε αυτούς τους Νόμους, το δεύτερο μέλος παύει να είναι πλέον μηδέν
και προκύπτει ένας νέος όρος που εμπεριέχει τον τελεστή
της "χρονικής παραγώγου" (d/dt)
Έτσι έχουμε
α) για τους Πεδιακούς Νόμους
β) για τους Νόμους Διατήρησης
Το αποτέλεσμα αυτό δεν καταστρέφει, απλά,
την αρμονία της Γεωμετροποίησης
όπως θα μπορούσε κάποιος να υποθέσει,
αφελώς, σε πρώτη εκτίμηση,
αλλά "συντρίβει" και όλο το οικοδόμημα της Φυσικής του Ηλεκτρομαγνητισμού
και επιπλέον, παρασύρει ταυτόχρονα, στον όλεθρο, όλη τη Φυσική συνολικά
κάτι που θα εξηγήσουμε στο επόμενο.
-------------------------------------------------------------------
Όπως αναφέραμε στο προηγούμενο Μέρος C-01,
η "αρχειοθέτηση" σε πίνακες (Μέρος B-12a και Μέρος B-12b)
των Φυσικών Μεγεθών και των Φυσικών Νόμων
του Ηλεκτρομαγνητισμού, με βάση την Γεωμετροποίηση,
διαθέτει μία εξαιρετική αρμονία
(καθώς εμπεριέχει πολλές μαθηματικές συμμετρίες)
Όμως, η εμπλοκή του Χρόνου
αλλάζει ριζικά αυτήν την εικόνα
και κλονίζει "συθέμελα" την Γεωμετροποίηση.
Ας δούμε γιατί συμβαίνει αυτό.
Η "καταστροφή" οφείλεται
στην ανακάλυψη δύο κρίσιμων φαινομένων
- του φαινομένου της Ηλεκτρικής Μετατόπισης
(ή ορθότερα Φορτιακής Επαγωγής)
(ανακαλύφθηκε το 1861, από τον Maxwell)
- και του φαινομένου της Μαγνητικής Επαγωγής
(ανακαλύφθηκε το 1831 από τον Faraday)
1) Σύμφωνα με το Φαινόμενο της Ηλεκτρικής Μετατόπισης
που συμβαίνει σε έναν Πυκνωτή:
"Χρονικά μεταβαλλόμενο Ηλεκτρικό Φορτίο, δημιουργεί Ηλεκτρικό Ρεύμα"
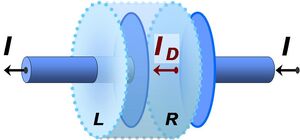 |
| Φαινόμενο Ηλεκτρικής Μετατόπισης (ή ορθότερα, "Φορτιακής Επαγωγής") ----- Μεταβαλλόμενο (με τον χρόνο) Ηλεκτρικό Φορτίο "επάγει" (δηλ. προκαλεί) (επαγωγικό) Ηλεκτρικό Ρεύμα (η αλλιώς "Ρεύμα Μετατόπισης") |
που συμβαίνει σε ένα Πηνίο:
"Χρονικά μεταβαλλόμενο Μαγνητικό Πεδίο, δημιουργεί Ηλεκτρικό Πεδίο"
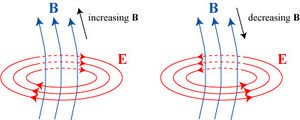 |
| Φαινόμενο Μαγνητικής Επαγωγής ---- Μεταβαλλόμενο (με τον χρόνο) Μαγνητικό Πεδίο "επάγει" (δηλ. προκαλεί) (επαγωγικό) Ηλεκτρικό Πεδίο |
- Ωραία, θα πει κάποιος, και ποιές είναι επιπτώσεις
αυτών των δύο φαινομένων?
Η πρώτη επίπτωση είναι ευπρόσδεκτη
και αναμενόμενη κατά κάποιον τρόπο
Αφορά την φύση ( = υφή) των "κβάντων" των 4 Οντοτήτων
Δηλαδή:
Δεν υπάρχει, πλέον,
- διάκριση μεταξύ "ακινήτων" και "κινούμενουν" ηλεκτρονίων
καθώς επίσης,
- ούτε και διάκριση μεταξύ "ακινήτων" και "κινούμενουν" φωτονίων
Ας δούμε τώρα ποιά είναι η επίπτωση στους Φυσικούς Νόμους
Όπως είναι λογικό, δεν υπάρχει καμία επίπτωση στους 8 Νόμους Σύνδεσης
και έτσι ο Πίνακας 1 μένει όπως έχει
Δεν υπάρχει επίπτωση στους Νόμους (Πεδιακούς και Διατήρησης)
του Ηλεκτρικού Φορτίου και του Μαγνητικού Πεδίου
κάτι που επίσης είναι αυτονόητο
καθώς δεν μπορούν να φυτρώνουν (ή να χάνονται)
- ούτε ηλεκτρόνια, δηλ. Ύλη
- ούτε φωτόνια, δηλ. Ενέργεια
από το (ή στο) "Πουθενά".
Οπότε, λογικά, οι δύο Φυσικοί Νόμοι (eq. 09 και eq. 11) του Πίνακα 2
(καθώς και οι 2x3 = 6 αντίστοιχοί τους από τους Πίνακες 3 και 4)
να παραμένουν ως έχουν
Υπάρχουν όμως επιπτώσεις στους Νόμους (Πεδιακούς και Διατήρησης)
του Ηλεκτρικού Ρεύματος και του Ηλεκτρικού Πεδίου.
Αυτοί που επηρεάζονται από τα δύο Φαινόμενα
είναι οι άλλοι δύο Φυσικοί Νόμοι του Πίνακα 2
(καθώς και οι 2x3 = 6 αντίστοιχοί τους από τους Πίνακες 3 και 4)
Σε αυτούς τους Νόμους, το δεύτερο μέλος παύει να είναι πλέον μηδέν
και προκύπτει ένας νέος όρος που εμπεριέχει τον τελεστή
της "χρονικής παραγώγου" (d/dt)
Έτσι έχουμε
α) για τους Πεδιακούς Νόμους
 |
| Προσθήκη λεζάντας |
β) για τους Νόμους Διατήρησης
 |
| Προσθήκη λεζάντας |
Το αποτέλεσμα αυτό δεν καταστρέφει, απλά,
την αρμονία της Γεωμετροποίησης
όπως θα μπορούσε κάποιος να υποθέσει,
αφελώς, σε πρώτη εκτίμηση,
αλλά "συντρίβει" και όλο το οικοδόμημα της Φυσικής του Ηλεκτρομαγνητισμού
και επιπλέον, παρασύρει ταυτόχρονα, στον όλεθρο, όλη τη Φυσική συνολικά
κάτι που θα εξηγήσουμε στο επόμενο.
 |
| Δεν υπάρχει παραστατικότερη εικόνα για να απεικονίσει την "καταστροφή' που επιφέρει ο Χρόνος στο μοντέλο της Γεωμετροποίησης |
-------------------------------------------------------------------
--------------------------------------------------------------------

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου