Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο26-
Αναζήτηση
"κρυμμένων" Διαστάσεων
(η' μέρος)
"κρυμμένων" Διαστάσεων
(η' μέρος)
--------------------------------------------------------------------
--------------------------------------------------------------------
Στο προηγούμενο μέρος, καταλήξαμε στο διάνυσμα θέσης του νέου Χωρόχρονου
-----
Απλά, και μόνον για λόγους σύγκρισης, ξαναγράφουμε εδώ
το διάνυσμα θέσης του 4D-Πραγματικού Χωρόχρονου Minkowski.
Συμπληρώνουμε εδώ
Ότι και ο νέος Χωρόχρονος είναι τύπου Minkowski
Όμως γιατί ο νέος αυτός Χωρόχρονος να είναι φανταστικός και όχι πραγματικός?
Η απάντηση στηρίζεται σε μία παρατήρηση
Στην Φύση υπάρχουν Σώματα αλλά και Κύματα.
Όλα αυτά περιγράφονται από Φυσικά Μεγέθη
(όπως τα είχαμε περιγράψει στο Μέρος 09)
Και για μεν, την μελέτη των Σωμάτων (και Σωματιδίων)
αρκεί ο γνωστός μας Πραγματικός 4D-Χωρόχρονος Minkowski
καθόσον όλα τα Φυσικά Μεγέθη που τα περιγράφουν
είναι πραγματικές συναρτήσεις των διαστάσεων (x, y, z, t)
Όμως, για την μελέτη των Κυμάτων (και των Κυματοσυρμών)
ο Πραγματικός Χώρος δεν αρκεί,
καθόσον όλα τα Φυσικά Μεγέθη που τα περιγράφουν
είναι μιγαδικές συναρτήσεις των γνωστών πραγματικών διαστάσεων (x, y, z, t)
αλλά και των νέων φανταστικών (ikx, iky, ikz, iω) (!)
Στο προηγούμενο μέρος, καταλήξαμε στο διάνυσμα θέσης του νέου Χωρόχρονου
 |
| όπου: τα καφετί x,y,z είναι τα μήκη κύματος στους 3 άξονες το πράσινο t δηλώνει την περίοδο του κύματος |
Απλά, και μόνον για λόγους σύγκρισης, ξαναγράφουμε εδώ
το διάνυσμα θέσης του 4D-Πραγματικού Χωρόχρονου Minkowski.
 |
| όπου: τα ερυθρά x,y,z είναι οι γνωστές συντεταγμένες του Χώρου και το γαλάζιο t είναι η διάσταση του Χρόνου |
Ότι και ο νέος Χωρόχρονος είναι τύπου Minkowski
Όμως γιατί ο νέος αυτός Χωρόχρονος να είναι φανταστικός και όχι πραγματικός?
Η απάντηση στηρίζεται σε μία παρατήρηση
Στην Φύση υπάρχουν Σώματα αλλά και Κύματα.
Όλα αυτά περιγράφονται από Φυσικά Μεγέθη
(όπως τα είχαμε περιγράψει στο Μέρος 09)
 |
| Τα Φυσικά Μεγέθη (π.χ. ταχύτητα, μάζα θερμοκρασία κλπ) είναι συναρτήσεις. Για κάθε σημείο του Χωρόχρονου που προσδιορίζεται από τις Διαστάσεις του (x,y,z,t) (στο σχήμα "inputs") προκύπτει και μία τιμή για το όποιο Φυσικό Μέγεθος (στο σχήμα outputs) |
αρκεί ο γνωστός μας Πραγματικός 4D-Χωρόχρονος Minkowski
καθόσον όλα τα Φυσικά Μεγέθη που τα περιγράφουν
είναι πραγματικές συναρτήσεις των διαστάσεων (x, y, z, t)
 |
| όπου: φ = ένα Φυσικό Μέγεθος της Σωματιδιακής Μηχανικής f = η συνάρτηση που το περιγράφει x,t = οι 4 συντεταγμένες του Πραγματικού Χωρόχρονου |
ο Πραγματικός Χώρος δεν αρκεί,
καθόσον όλα τα Φυσικά Μεγέθη που τα περιγράφουν
είναι μιγαδικές συναρτήσεις των γνωστών πραγματικών διαστάσεων (x, y, z, t)
αλλά και των νέων φανταστικών (ikx, iky, ikz, iω) (!)
 |
| όπου: ψ = ένα Φυσικό Μέγεθος της Κυματικής f = η συνάρτηση που το περιγράφει x,t = οι 4 συντεταγμένες του Πραγματικού Χωρόχρονου k, ω = οι 4 συντεταγμένες του Φανταστικού Χωρόχρονου |
Η διαφορά των Φυσικών Μεγεθών που περιγράφουν Σώματα
και αυτών που περιγράφουν Κύματα
οφείλεται προφανώς στην "εκθετική συνάρτηση" (exp)
Ας δούμε, λοιπόν, αυτήν την εκθετική συνάρτηση (exp), καλύτερα.
Ο Euler βρήκε έναν έναν εντυπωσιακό τύπο (τύπος του Euler)
που δείχνει ακριβώς την υφή της.
Ας το δούμε αυτήν την ανάλυση σχηματικά:
Ας δούμε τώρα την εξέλιξη της εκθετικής συνάρτησης στο χρόνο
Αναρωτιέται κανείς
μα πως τόσα χρόνια, τόσους αιώνες δεν το είδαμε, δεν το αντιληφθήκαμε,
δεν μας πέρασε από το μυαλό
ότι μπορεί να υπάρχει (εκτός από τον Πραγματικό) και Φανταστικός Χώρος?
Απλά, δεν είχαν ωριμάσει οι συνθήκες
Έπρεπε να έρθει η Χορδοθεωρία για να μας ανοίξει τα μάτια.
Και όμως ...
είχαμε βρει τους Μιγαδικούς Αριθμούς
Έτσι είναι η Φυσική.
Άμα βρεθεί κάτι σου φαίνεται προφανέστατο.
Πριν βρεθεί είναι άπιαστο...
Εδώ χρειάζεται μία διευκρίνηση
Και καλά από που κατέβηκαν αυτοί οι Φανταστικοί Αριθμοί?
Πως μπλέχτηκαν στα πόδια μας?
Μήπως είναι φαντάσματα?
Όχι. Είναι υπαρκτοί όσο και οι Πραγματικοί Αριθμοί.
Είναι, απλά, "θύματα" του ονόματος που εμείς οι Άνθρωποι τους δώσαμε.
-------------------------------------------------------------------
και αυτών που περιγράφουν Κύματα
οφείλεται προφανώς στην "εκθετική συνάρτηση" (exp)
Ας δούμε, λοιπόν, αυτήν την εκθετική συνάρτηση (exp), καλύτερα.
Ο Euler βρήκε έναν έναν εντυπωσιακό τύπο (τύπος του Euler)
που δείχνει ακριβώς την υφή της.
 |
| Η εκθετική συνάρτηση (exp) είναι μιγαδική Αναλύεται: - σε ένα πραγματικό μέρος, δηλ. την συνημιτονοειδή συνάρτηση (cos) και - σε ένα φανταστικό μέρος, δηλ. την ημίτονοειδή συνάρτηση (sin) |
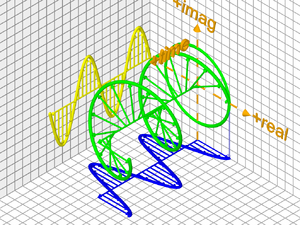 |
| H εκθετική συνάρτηση (exp) απεικονίζεται από τον πράσινο έλικα - το πραγματικό της τμήμα προβάλλεται στο "οριζόντιο δάπεδο" και απεικονίζεται από την γαλάζια συνάρτηση (cos) - το φανταστικό της τμήμα προβάλλεται στον "κάθετο τοίχο" και απεικονίζεται από την κίτρινη συνάρτηση (sin) |
Ας δούμε τώρα την εξέλιξη της εκθετικής συνάρτησης στο χρόνο
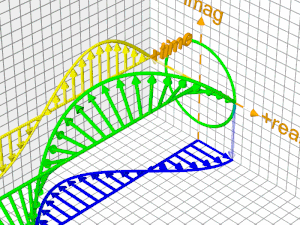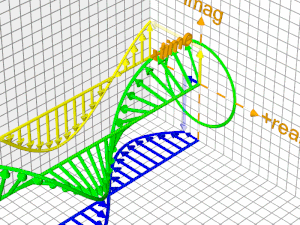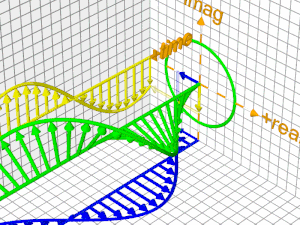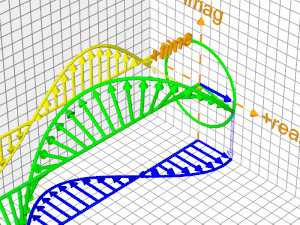 |
| Εδώ φαίνεται καθαρά Η εκθετική συνάρτηση (exp) είναι "πλάσμα" του Ενιαίου Χώρου (του Φασικού, όπως συνήθως αποκαλείται) ενώ η συνημιτοειδής συνάρτηση (cos) είναι "πλάσμα" του Πραγματικού Χώρου (στον οποίο ζούμε και οι Άνθρωποι ως σώματα) ή ακριβέστερα, η προβολή της εκθετικής στον Πραγματικό Χώρο και η ημιτονοειδής συνάρτηση (sin) είναι "πλάσμα" του Φανταστικού Χώρου (στον οποίο έχουν πρόσβαση μόνον τα Κύματα και όχι τα Σώματα) ή ακριβέστερα, η προβολή της εκθετικής στον Φανταστικό Χώρο |
Αναρωτιέται κανείς
μα πως τόσα χρόνια, τόσους αιώνες δεν το είδαμε, δεν το αντιληφθήκαμε,
δεν μας πέρασε από το μυαλό
ότι μπορεί να υπάρχει (εκτός από τον Πραγματικό) και Φανταστικός Χώρος?
Απλά, δεν είχαν ωριμάσει οι συνθήκες
Έπρεπε να έρθει η Χορδοθεωρία για να μας ανοίξει τα μάτια.
Και όμως ...
είχαμε βρει τους Μιγαδικούς Αριθμούς
 |
| Κάθε μιγαδικός αριθμός (z) αναλύεται σε έναν Πραγματικό Αριθμό (a) και σε ένα Φανταστικό Αριθμό (b) με την βοήθεια της φανταστικής μονάδας (i) |
Γιατί, λοιπόν, δεν αναρωτηθήκαμε για το ενδεχόμενο
και οι Διαστάσεις να είναι μιγαδικές (complex)?
- Γιατί να είναι μόνον πραγματικές (real) ?
- Γιατί να μην έχουν και ένα φανταστικό (imaginary) μέρος?
Ευνόητα ερωτήματα κατόπιν εορτής.
Άμα βρεθεί κάτι σου φαίνεται προφανέστατο.
Πριν βρεθεί είναι άπιαστο...
Εδώ χρειάζεται μία διευκρίνηση
Και καλά από που κατέβηκαν αυτοί οι Φανταστικοί Αριθμοί?
Πως μπλέχτηκαν στα πόδια μας?
Μήπως είναι φαντάσματα?
Όχι. Είναι υπαρκτοί όσο και οι Πραγματικοί Αριθμοί.
Είναι, απλά, "θύματα" του ονόματος που εμείς οι Άνθρωποι τους δώσαμε.
 |
Όσο λύναμε εξισώσεις
της μορφής
x στο τετράγωνο = 1
δεν είχαμε πρόβλημα.
Είχαμε μία θετική και μία αρνητική λύση
Όμως,
όταν η Φυσική ζήτησε να λύσουμε εξισώσεις
της μορφής
x στο τετράγωνο = -1
τότε βρεθήκαμε σε αδιέξοδο
Έτσι ανακαλύψαμε την ρίζα του -1 δηλ. το i
και μαζί του τους Φανταστικούς Αριθμούς
|
--------------------------------------------------------------------

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου